# 为什么 MySQL 采用 B+ 树作为索引?
大家好,我是小林。
「为什么 MySQL 采用 B+ 树作为索引?」这句话,是不是在面试时经常出现。
要解释这个问题,其实不单单要从数据结构的角度出发,还要考虑磁盘 I/O 操作次数,因为 MySQL 的数据是存储在磁盘中的嘛。
这次,就跟大家一层一层的分析这个问题,图中包含大量的动图来帮助大家理解,相信看完你就拿捏这道题目了!
# 怎样的索引的数据结构是好的?
MySQL 的数据是持久化的,意味着数据(索引+记录)是保存到磁盘上的,因为这样即使设备断电了,数据也不会丢失。
磁盘是一个慢的离谱的存储设备,有多离谱呢?
人家内存的访问速度是纳秒级别的,而磁盘访问的速度是毫秒级别的,也就是说读取同样大小的数据,磁盘中读取的速度比从内存中读取的速度要慢上万倍,甚至几十万倍。
磁盘读写的最小单位是扇区,扇区的大小只有 512B 大小,操作系统一次会读写多个扇区,所以操作系统的最小读写单位是块(Block)。Linux 中的块大小为 4KB,也就是一次磁盘 I/O 操作会直接读写 8 个扇区。
由于数据库的索引是保存到磁盘上的,因此当我们通过索引查找某行数据的时候,就需要先从磁盘读取索引到内存,再通过索引从磁盘中找到某行数据,然后读入到内存,也就是说查询过程中会发生多次磁盘 I/O,而磁盘 I/O 次数越多,所消耗的时间也就越大。
所以,我们希望索引的数据结构能在尽可能少的磁盘的 I/O 操作中完成查询工作,因为磁盘 I/O 操作越少,所消耗的时间也就越小。
另外,MySQL 是支持范围查找的,所以索引的数据结构不仅要能高效地查询某一个记录,而且也要能高效地执行范围查找。
所以,要设计一个适合 MySQL 索引的数据结构,至少满足以下要求:
- 能在尽可能少的磁盘的 I/O 操作中完成查询工作;
- 要能高效地查询某一个记录,也要能高效地执行范围查找;
分析完要求后,我们针对每一个数据结构分析一下。
# 什么是二分查找?
索引数据最好能按顺序排列,这样可以使用「二分查找法」高效定位数据。
假设我们现在用数组来存储索引,比如下面有一个排序的数组,如果要从中找出数字 3,最简单办法就是从头依次遍历查询,这种方法的时间复杂度是 O(n),查询效率并不高。因为该数组是有序的,所以我们可以采用二分查找法,比如下面这张采用二分法的查询过程图:

可以看到,二分查找法每次都把查询的范围减半,这样时间复杂度就降到了 O(logn),但是每次查找都需要不断计算中间位置。
# 什么是二分查找树?
用数组来实现线性排序的数据虽然简单好用,但是插入新元素的时候性能太低。
因为插入一个元素,需要将这个元素之后的所有元素后移一位,如果这个操作发生在磁盘中呢?这必然是灾难性的。因为磁盘的速度比内存慢几十万倍,所以我们不能用一种线性结构将磁盘排序。
其次,有序的数组在使用二分查找的时候,每次查找都要不断计算中间的位置。
那我们能不能设计一个非线形且天然适合二分查找的数据结构呢?
有的,请看下图这个神奇的操作,找到所有二分查找中用到的所有中间节点,把他们用指针连起来,并将最中间的节点作为根节点。

怎么样?是不是变成了二叉树,不过它不是普通的二叉树,它是一个二叉查找树。
二叉查找树的特点是一个节点的左子树的所有节点都小于这个节点,右子树的所有节点都大于这个节点,这样我们在查询数据时,不需要计算中间节点的位置了,只需将查找的数据与节点的数据进行比较。
假设,我们查找索引值为 key 的节点:
- 如果 key 大于根节点,则在右子树中进行查找;
- 如果 key 小于根节点,则在左子树中进行查找;
- 如果 key 等于根节点,也就是找到了这个节点,返回根节点即可。
二叉查找树查找某个节点的动图演示如下,比如要查找节点 3 :
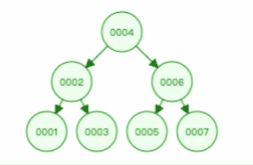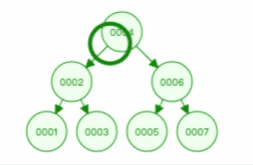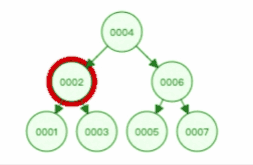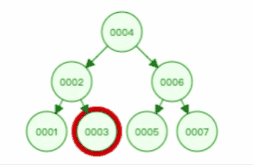
另外,二叉查找树解决了插入新节点的问题,因为二叉查找树是一个跳跃结构,不必连续排列。这样在插入的时候,新节点可以放在任何位置,不会像线性结构那样插入一个元素,所有元素都需要向后排列。
下面是二叉查找树插入某个节点的动图演示:

因此,二叉查找树解决了连续结构插入新元素开销很大的问题,同时又保持着天然的二分结构。
那是不是二叉查找树就可以作为索引的数据结构了呢?
不行不行,二叉查找树存在一个极端情况,会导致它变成一个瘸子!
当每次插入的元素都是二叉查找树中最大的元素,二叉查找树就会退化成了一条链表,查找数据的时间复杂度变成了 O(n),如下动图演示:

由于树是存储在磁盘中的,访问每个节点,都对应一次磁盘 I/O 操作(假设一个节点的大小「小于」操作系统的最小读写单位块的大小),也就是说树的高度就等于每次查询数据时磁盘 IO 操作的次数,所以树的高度越高,就会影响查询性能。
二叉查找树由于存在退化成链表的可能性,会使得查询操作的时间复杂度从 O(logn) 升为 O(n)。
而且会随着插入的元素越多,树的高度也变高,意味着需要磁盘 IO 操作的次数就越多,这样导致查询性能严重下降,再加上不能范围查询,所以不适合作为数据库的索引结构。
# 什么是自平衡二叉树?
为了解决二叉查找树会在极端情况下退化成链表的问题,后面就有人提出平衡二叉查找树(AVL 树)。
主要是在二叉查找树的基础上增加了一些条件约束:每个节点的左子树和右子树的高度差不能超过 1。也就是说节点的左子树和右子树仍然为平衡二叉树,这样查询操作的时间复杂度就会一直维持在 O(logn) 。
下图是每次插入的元素都是平衡二叉查找树中最大的元素,可以看到,它会维持自平衡:
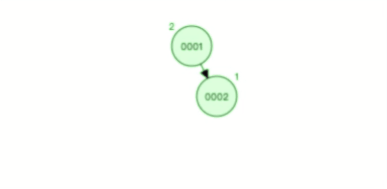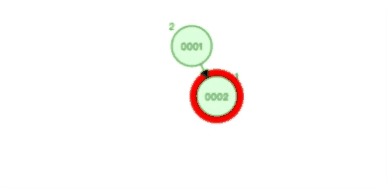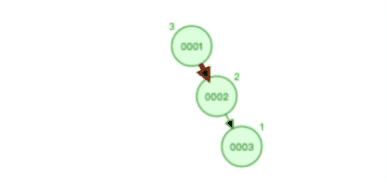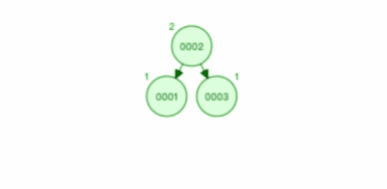
除了平衡二叉查找树,还有很多自平衡的二叉树,比如红黑树,它也是通过一些约束条件来达到自平衡,不过红黑树的约束条件比较复杂,不是本篇的重点重点,大家可以看《数据结构》相关的书籍来了解红黑树的约束条件。
下面是红黑树插入节点的过程,这左旋右旋的操作,就是为了自平衡。
不管平衡二叉查找树还是红黑树,都会随着插入的元素增多,而导致树的高度变高,这就意味着磁盘 I/O 操作次数多,会影响整体数据查询的效率。
比如,下面这个平衡二叉查找树的高度为 5,那么在访问最底部的节点时,就需要磁盘 5 次 I/O 操作。
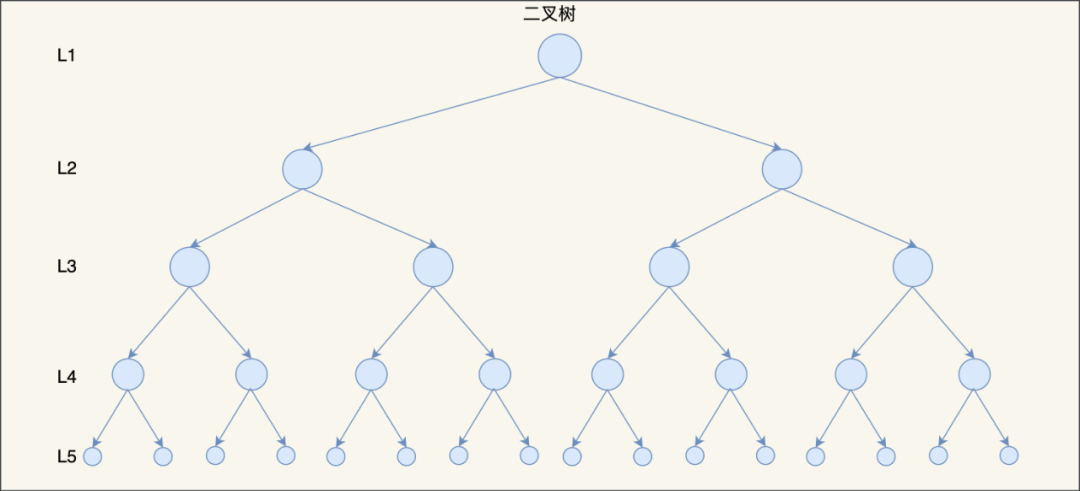
根本原因是因为它们都是二叉树,也就是每个节点只能保存 2 个子节点 ,如果我们把二叉树改成 M 叉树(M>2)呢?
比如,当 M=3 时,在同样的节点个数情况下,三叉树比二叉树的树高要矮。
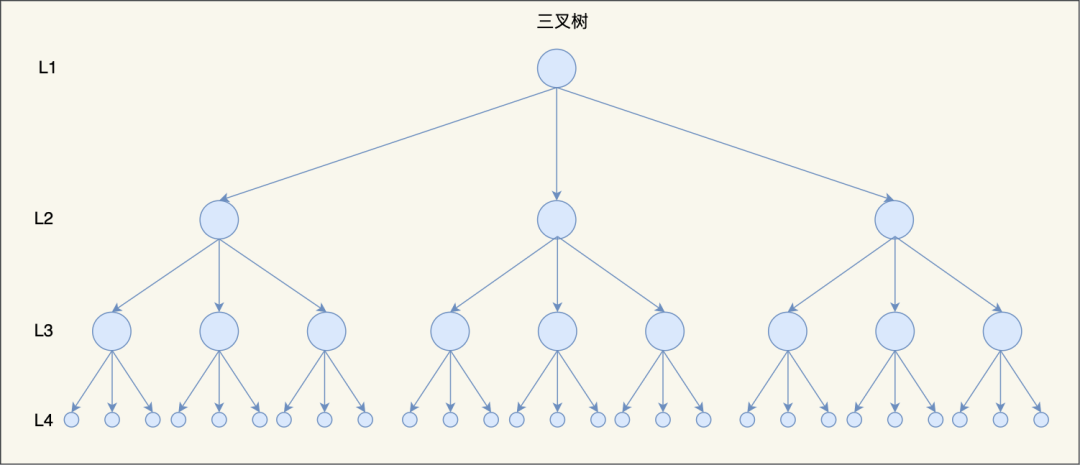
因此,当树的节点越多的时候,并且树的分叉数 M 越大的时候,M 叉树的高度会远小于二叉树的高度。
# 什么是 B 树
自平衡二叉树虽然能保持查询操作的时间复杂度在O(logn),但是因为它本质上是一个二叉树,每个节点只能有 2 个子节点,那么当节点个数越多的时候,树的高度也会相应变高,这样就会增加磁盘的 I/O 次数,从而影响数据查询的效率。
为了解决降低树的高度的问题,后面就出来了 B 树,它不再限制一个节点就只能有 2 个子节点,而是允许 M 个子节点 (M>2),从而降低树的高度。
B 树的每一个节点最多可以包括 M 个子节点,M 称为 B 树的阶,所以 B 树就是一个多叉树。
假设 M = 3,那么就是一棵 3 阶的 B 树,特点就是每个节点最多有 2 个(M-1个)数据和最多有 3 个(M个)子节点,超过这些要求的话,就会分裂节点,比如下面的的动图:

我们来看看一棵 3 阶的 B 树的查询过程是怎样的?
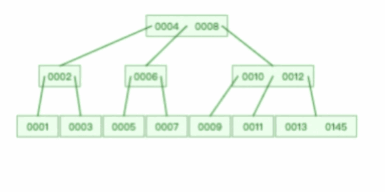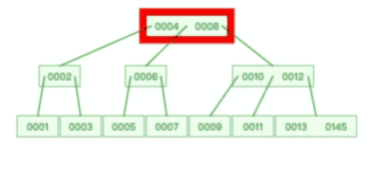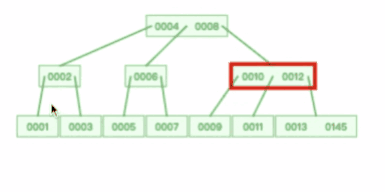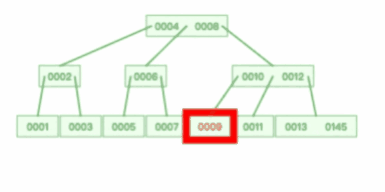
假设我们在上图一棵 3 阶的 B 树中要查找的索引值是 9 的记录那么步骤可以分为以下几步:
- 与根节点的索引(4,8)进行比较,9 大于 8,那么往右边的子节点走;
- 然后该子节点的索引为(10,12),因为 9 小于 10,所以会往该节点的左边子节点走;
- 走到索引为9的节点,然后我们找到了索引值 9 的节点。
可以看到,一棵 3 阶的 B 树在查询叶子节点中的数据时,由于树的高度是 3 ,所以在查询过程中会发生 3 次磁盘 I/O 操作。
而如果同样的节点数量在平衡二叉树的场景下,树的高度就会很高,意味着磁盘 I/O 操作会更多。所以,B 树在数据查询中比平衡二叉树效率要高。
但是 B 树的每个节点都包含数据(索引+记录),而用户的记录数据的大小很有可能远远超过了索引数据,这就需要花费更多的磁盘 I/O 操作次数来读到「有用的索引数据」。
而且,在我们查询位于底层的某个节点(比如 A 记录)过程中,「非 A 记录节点」里的记录数据会从磁盘加载到内存,但是这些记录数据是没用的,我们只是想读取这些节点的索引数据来做比较查询,而「非 A 记录节点」里的记录数据对我们是没用的,这样不仅增多磁盘 I/O 操作次数,也占用内存资源。
另外,如果使用 B 树来做范围查询的话,需要使用中序遍历,这会涉及多个节点的磁盘 I/O 问题,从而导致整体速度下降。
# 什么是 B+ 树?
B+ 树就是对 B 树做了一个升级,MySQL 中索引的数据结构就是采用了 B+ 树,B+ 树结构如下图:
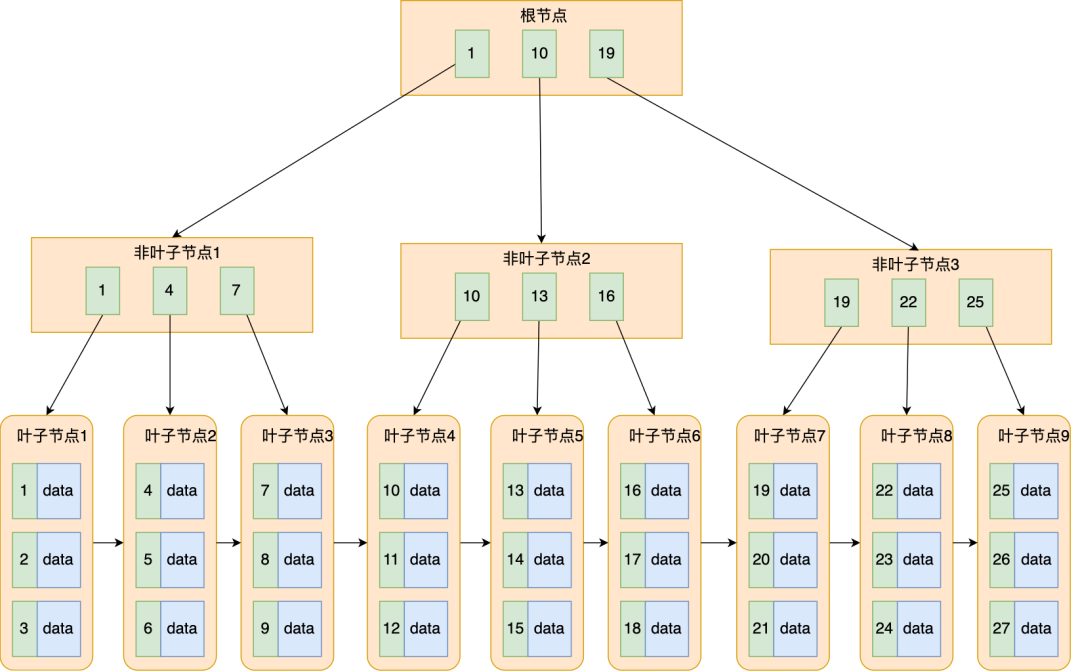
B+ 树与 B 树差异的点,主要是以下这几点:
- 叶子节点(最底部的节点)才会存放实际数据(索引+记录),非叶子节点只会存放索引;
- 所有索引都会在叶子节点出现,叶子节点之间构成一个有序链表;
- 非叶子节点的索引也会同时存在在子节点中,并且是在子节点中所有索引的最大(或最小)。
- 非叶子节点中有多少个子节点,就有多少个索引;
下面通过三个方面,比较下 B+ 和 B 树的性能区别。
# 1、单点查询
B 树进行单个索引查询时,最快可以在 O(1) 的时间代价内就查到,而从平均时间代价来看,会比 B+ 树稍快一些。
但是 B 树的查询波动会比较大,因为每个节点即存索引又存记录,所以有时候访问到了非叶子节点就可以找到索引,而有时需要访问到叶子节点才能找到索引。
B+ 树的非叶子节点不存放实际的记录数据,仅存放索引,因此数据量相同的情况下,相比存储即存索引又存记录的 B 树,B+树的非叶子节点可以存放更多的索引,因此 B+ 树可以比 B 树更「矮胖」,查询底层节点的磁盘 I/O次数会更少。
# 2、插入和删除效率
B+ 树有大量的冗余节点,这样使得删除一个节点的时候,可以直接从叶子节点中删除,甚至可以不动非叶子节点,这样删除非常快,
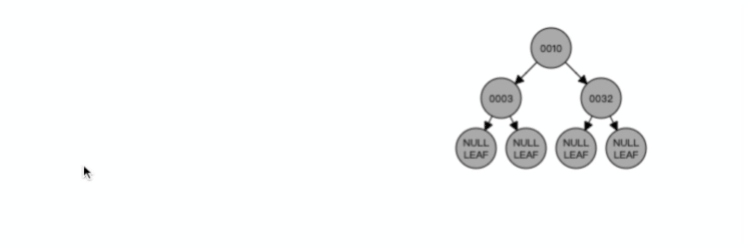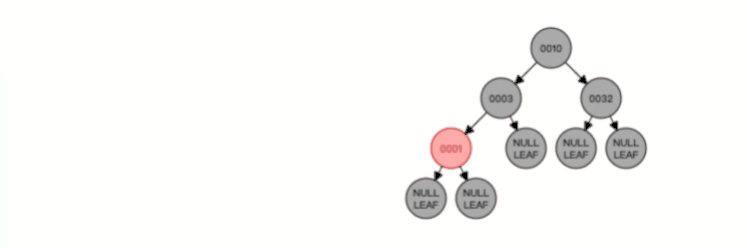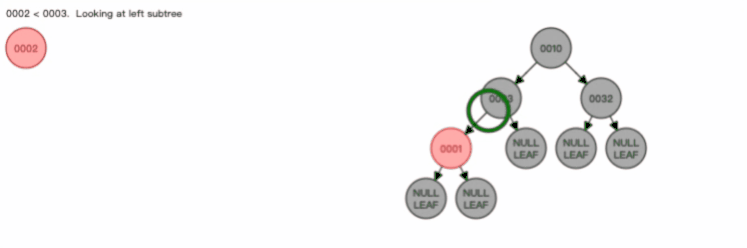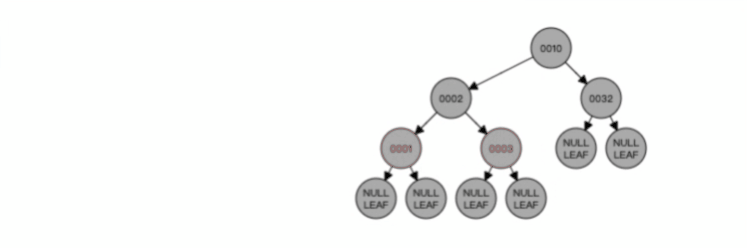
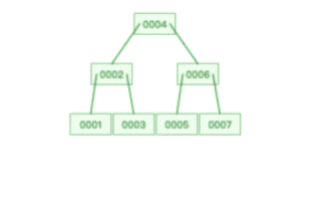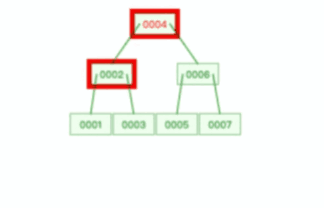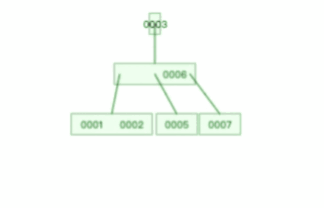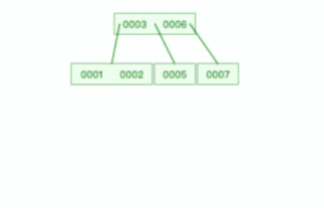
比如下面这个动图是删除 B+ 树 0004 节点的过程,因为非叶子节点有 0004 的冗余节点,所以在删除的时候,树形结构变化很小:
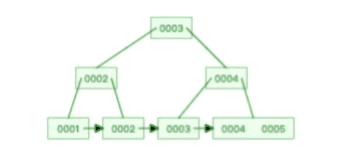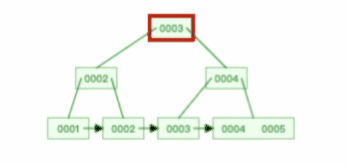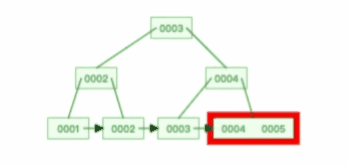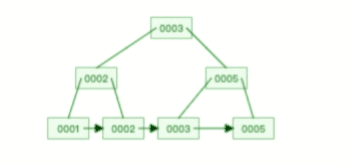
注意,:B+ 树对于非叶子节点的子节点和索引的个数,定义方式可能会有不同,有的是说非叶子节点的子节点的个数为 M 阶,而索引的个数为 M-1(这个是维基百科里的定义),因此我本文关于 B+ 树的动图都是基于这个。但是我在前面介绍 B 树与 B+ 树的差异时,说的是「非叶子节点中有多少个子节点,就有多少个索引」,主要是 MySQL 用到的 B+ 树就是这个特性。
下面这个动图是删除 B 树 0008 节点的过程,可能会导致树的复杂变化:
甚至,B+ 树在删除根节点的时候,由于存在冗余的节点,所以不会发生复杂的树的变形,比如下面这个动图是删除 B+ 树根节点的过程:
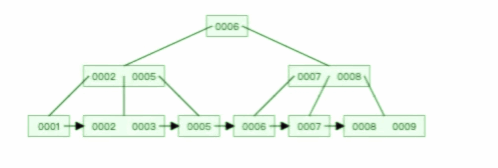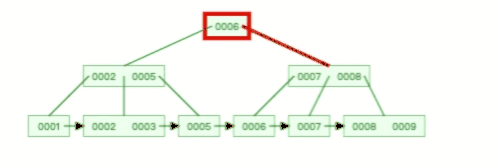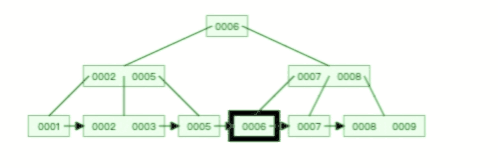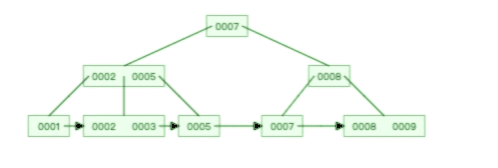
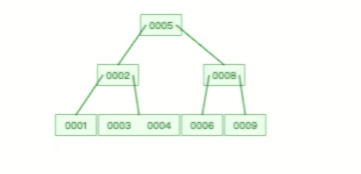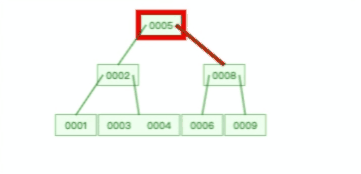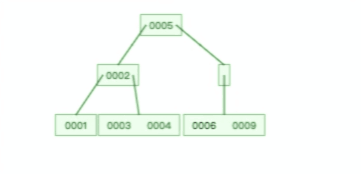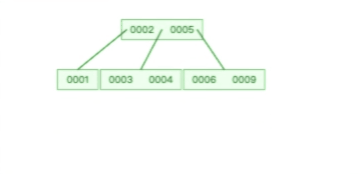
B 树则不同,B 树没有冗余节点,删除节点的时候非常复杂,比如删除根节点中的数据,可能涉及复杂的树的变形,比如下面这个动图是删除 B 树根节点的过程:
B+ 树的插入也是一样,有冗余节点,插入可能存在节点的分裂(如果节点饱和),但是最多只涉及树的一条路径。而且 B+ 树会自动平衡,不需要像更多复杂的算法,类似红黑树的旋转操作等。
因此,B+ 树的插入和删除效率更高。
# 3、范围查询
B 树和 B+ 树等值查询原理基本一致,先从根节点查找,然后对比目标数据的范围,最后递归的进入子节点查找。
因为 B+ 树所有叶子节点间还有一个链表进行连接,这种设计对范围查找非常有帮助,比如说我们想知道 12 月 1 日和 12 月 12 日之间的订单,这个时候可以先查找到 12 月 1 日所在的叶子节点,然后利用链表向右遍历,直到找到 12 月12 日的节点,这样就不需要从根节点查询了,进一步节省查询需要的时间。
而 B 树没有将所有叶子节点用链表串联起来的结构,因此只能通过树的遍历来完成范围查询,这会涉及多个节点的磁盘 I/O 操作,范围查询效率不如 B+ 树。
因此,存在大量范围检索的场景,适合使用 B+树,比如数据库。而对于大量的单个索引查询的场景,可以考虑 B 树,比如 nosql 的MongoDB。
# MySQL 中的 B+ 树
MySQL 的存储方式根据存储引擎的不同而不同,我们最常用的就是 Innodb 存储引擎,它就是采用了 B+ 树作为了索引的数据结构。
下图就是 Innodb 里的 B+ 树:
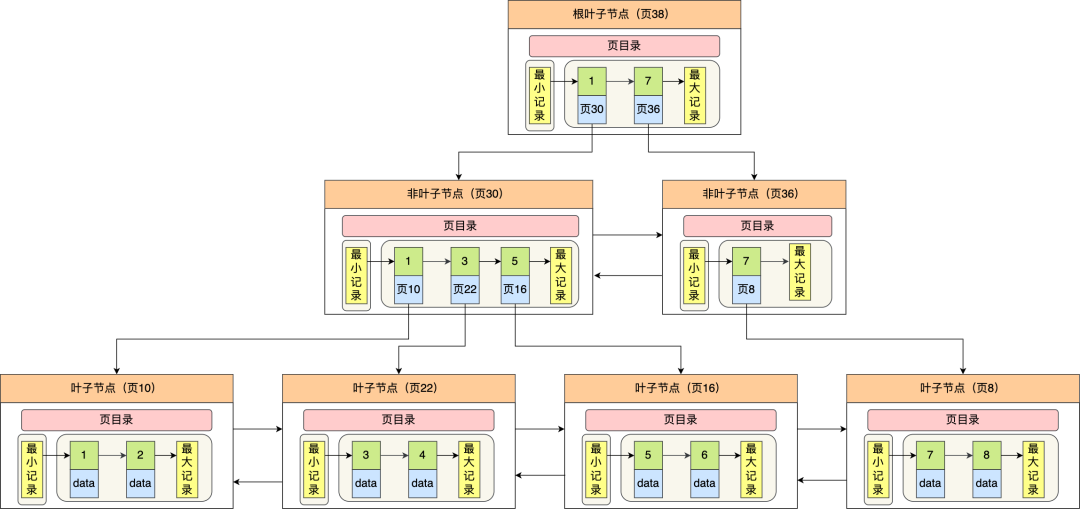
但是 Innodb 使用的 B+ 树有一些特别的点,比如:
- B+ 树的叶子节点之间是用「双向链表」进行连接,这样的好处是既能向右遍历,也能向左遍历。
- B+ 树节点内容是数据页,数据页里存放了用户的记录以及各种信息,每个数据页默认大小是 16 KB。
Innodb 根据索引类型不同,分为聚簇和二级索引。他们区别在于:
- 聚簇索引的叶子节点存放的是实际数据,所有完整的用户记录都存放在聚簇索引的叶子节点
- 而二级索引的叶子节点存放的是主键值,而不是实际数据。
因为表的数据都是存放在聚簇索引的叶子节点里,所以 InnoDB 存储引擎一定会为表创建一个聚簇索引,且由于数据在物理上只会保存一份,所以聚簇索引只能有一个,而二级索引可以创建多个。
更多关于 Innodb 的 B+ 树,可以看我之前写的这篇:从数据页的角度看 B+ 树 (opens new window)。
# 总结
MySQL 是会将数据持久化在硬盘,而存储功能是由 MySQL 存储引擎实现的,所以讨论 MySQL 使用哪种数据结构作为索引,实际上是在讨论存储引使用哪种数据结构作为索引,InnoDB 是 MySQL 默认的存储引擎,它就是采用了 B+ 树作为索引的数据结构。
要设计一个 MySQL 的索引数据结构,不仅仅考虑数据结构增删改的时间复杂度,更重要的是要考虑磁盘 I/0 的操作次数。因为索引和记录都是存放在硬盘,硬盘是一个非常慢的存储设备,我们在查询数据的时候,最好能在尽可能少的磁盘 I/0 的操作次数内完成。
二分查找树虽然是一个天然的二分结构,能很好的利用二分查找快速定位数据,但是它存在一种极端的情况,每当插入的元素都是树内最大的元素,就会导致二分查找树退化成一个链表,此时查询复杂度就会从 O(logn)降低为 O(n)。
为了解决二分查找树退化成链表的问题,就出现了自平衡二叉树,保证了查询操作的时间复杂度就会一直维持在 O(logn) 。但是它本质上还是一个二叉树,每个节点只能有 2 个子节点,随着元素的增多,树的高度会越来越高。
而树的高度决定于磁盘 I/O 操作的次数,因为树是存储在磁盘中的,访问每个节点,都对应一次磁盘 I/O 操作,也就是说树的高度就等于每次查询数据时磁盘 IO 操作的次数,所以树的高度越高,就会影响查询性能。
B 树和 B+ 都是通过多叉树的方式,会将树的高度变矮,所以这两个数据结构非常适合检索存于磁盘中的数据。
但是 MySQL 默认的存储引擎 InnoDB 采用的是 B+ 作为索引的数据结构,原因有:
- B+ 树的非叶子节点不存放实际的记录数据,仅存放索引,因此数据量相同的情况下,相比存储即存索引又存记录的 B 树,B+树的非叶子节点可以存放更多的索引,因此 B+ 树可以比 B 树更「矮胖」,查询底层节点的磁盘 I/O次数会更少。
- B+ 树有大量的冗余节点(所有非叶子节点都是冗余索引),这些冗余索引让 B+ 树在插入、删除的效率都更高,比如删除根节点的时候,不会像 B 树那样会发生复杂的树的变化;
- B+ 树叶子节点之间用链表连接了起来,有利于范围查询,而 B 树要实现范围查询,因此只能通过树的遍历来完成范围查询,这会涉及多个节点的磁盘 I/O 操作,范围查询效率不如 B+ 树。
完!
最新的图解文章都在公众号首发,别忘记关注哦!!如果你想加入百人技术交流群,扫码下方二维码回复「加群」。
